ГЛАВА 2. КОНЦЕПТЫ И ТЕРМИНОЛОГИЯ

Чтобы понять кибернетические реальности больших систем управления, нам неизбежно придется порвать с общим стилем мышления, использованным в первой главе. Если существуют принципы управления, то следует начать с их точного определения. Это будет сделано исходя из того, что концепты и термины, известные в классической науке управления, мало чем нам помогут. В этой главе мы, следовательно, начнем обсуждение систем и управления ими на новом языке, без особых ссылок на деятельность фирм. Идея сводится к тому, чтобы сесть и подумать всерьез. Что такое собственно говоря управление?

Первый принцип управления сводится к тому, что управляющий является частью управляемой им системы. Управляющий не является человеком, посаженным над системой высшей властью, который в дальнейшем реализует свои полномочия. В любой системе, говорим ли мы о популяции животных или внутренних функциях живого организма, функции управления распределены по всей архитектуре системы. Управление совершенно невозможно отделить от организма, но его присутствие вытекает из поведения самой системы. Более того, управление совершенствуется с ростом системы и, если оглянуться на историю, то станет видно, что и управляющий развивался вместе с системой.

По этой причине лучше спрашивать о том, как система узнает о себе и своем состоянии, чем спрашивать, как управляющий узнает то же самое. Я полагаю, что нам не следует рисковать, отождествляя систему с личностью или с чем-то другим, лучше принять за систему те границы, в которых ее различает обозреватель. Будем далее определять состояние системы по ее поведению, то есть выделять в ее поведении то, что можно считать типичным для любой действующей системы. Примем систему как данное. Мы определим набор частей как систему, постольку поскольку эти части выступают как действующие в единстве. Примем ее обычную деятельность за примерное отображение ее естественной динамики. Иначе говоря, тот случай, когда ее части действуют типичным образом. Далее посмотрим, что произойдет, если мы вмешаемся - воткнем палку в систему, прикрикнем на нее или изменим окружающую ее температуру? Если система как-то ответит на эти стимулы, то можно сказать, что это действующая система. Заметьте, нем не нужно говорить, что система реагирует на эти стимулы, поскольку это требует целенаправленных действий по отношению к окружающему миру. Все, что мы узнали из этого эксперимента, сводится к тому, что системы чувствуют вмешательство в нее.Эта разница очень важна.

Подобное объяснение вызывает новый вопрос - что считать ответом на стимулы? Если мы вмешаемся в работающий автомобильный мотор путем выключения его зажигания, то будет ли верным заявить, что система ответила остановкой? Нет, поскольку мы разрушили динамическую систему, изучаемую нами, а не внесли в нее стимулы. Если мы пристрелили животное, оно умрет по той же причине. В равной мере, если мы бросили спичку на блок цилиндров автомобильного мотора или на спину слону, то ничего не произойдет. На этот раз потому, что наше вмешательство нельзя признать стимулом.

Не трудно уловить смысл вышесказанного. Ясно, что за стимул следует принимать такое вмешательство, которое так или иначе отражается на действиях системы, будучи не слишком скромным, чтобы не отразиться на ее деятельности, и не слишком сильным, чтобы ее разрушить. За реакцию системы примем некоторое ее изменение, имеющее смысл только в терминах использованного стимула. Если система изменится произвольно, при введении в нее того, что мы приняли за стимул, то вероятно какие-то изменения последуют. Кот, покинувший комнату, после того как он увидел плакат "Поди прочь" не отреагировал на содержание надписи и, следовательно, по нашему определению, для него такой плакат не является стимулом. Но мы вполне можем натренировать кота покидать комнату всякий раз, когда он увидит этот плакат. Если он станет всякий раз убегать из комнаты, то нам придется оставить идею о случайном совпадении и говорить о его реакции на стимул, о коте как действующей системе.

Из этого рассуждения вытекает несколько важных принципов управления. Стимулом является то, что изменяет работу системы. Реакция системы есть ее действие, которое должно интерпретироваться в терминах стимулов. В общем, это означает, что система избегает или как-то по другому противодействует стимулам, которые нарушают ее деятельность, и воспринимает или стремится усилить стимулы, которые способствуют ее деятельности. Заметим, что мы считаем очевидным, что наблюдаемые нами действия системы не являются случайными. Такое суждение зависит от того, насколько сильно проявляются качества системы при вмешательстве (что может ввести в заблуждение) или на высоконадежные показатели их повторяемости (это является научным критерием). Система, подтверждающая такое ее поведение, является действенной, по крайней мере до известной степени. Если она подтверждает такое свое поведение при всех обстоятельствах, мы будем называть ее действующей без всякого сомнения или оговорок. Это не будет безнадежно антинаучным суждением, поскольку вселенной управляют вероятности, а не абсолюты. В физике, в генетике, в общественных науках мы полагаемся на описания и даже на законы, которые основаны на балансе случайностей. Только в специальных или искусственно созданных областях, таких как теоретическая механика, эффект следует за причиной детерминированно и считается совершенно неизбежным. Но даже и здесь бывают исключения.

В общем, мы утверждаем, что реакция действующих систем на стимулы бывает либо негативной либо позитивной. В первом случае система склонна избегать враждебных ей стимулов, во втором - усиливать благоприятные стимулы. Из этого еле, что действующая система обладает, в известном смысле, возможностью судить о том, что к чему. Необходимо с осторожностью подходить к пониманию этого вывода. Действенность по-прежнему не эквивалентна самосознанию; система не обязана судить о важности стимулов. Все, что ей нужно, так это механизм, регистрирующий полезность или вредность стимулов, но эти термины в данном случае не несут этический нагрузки. Если система обладает критерием устойчивой работы, она может быть организована для работы по благоприятному для нее критерии Мы с самого начала заявляли: "возьмите некоторое обычное действие в качестве типичного для естественной динамики системы" - в этом и заключается ключ к пониманию управления. Системы существуют и они работают, если нет, то они не системы. Управление есть то, что способствует существованию и работе систем. Мы говорили и раньше, что быть действующей и воспринимать стимулы - две разные вещи. Посмотрим теперь почему. Так происходит потому, что критерием хорошей работы является критерий, основанный на внутренней стабильности. Можно предположить, что стимулы появляются из внешнего окружения системы; неразумные системы этого не знают, разумные система либо сами делают такое заключение, либо предчувствуют подобный факт. Но даже в подобном случае для обеих систем управляющее действие является ответом на внутреннее изменение, после того как система так или иначе его зарегистрировала. Мы отстраняемся от боли - это психологический факт, как и съеживаемся при виде шприца или горящей сигареты - интеллектуальная конструкция. В действительности мы съеживаемся от предчувствия боли, от предчувствия, существующего внутри нас, поскольку боль может испортить наше внутреннее состояние. Мы съеживаемся до того как почувствовали боль, поскольку видим приближающуюся опасность и просто понимаем внутренне последствия такой опасности, как прогноз внутренних событий. Так происходит потому, что мы (усовершенствованная) обучающаяся система. Если бы мы не научились связывать внешние события с их внутренними для нас последствиями, то мы бы не съеживались заранее. Типично, что наши представления об управлении довольно путаны, потому что мы сами системы весьма совершенные и мы знаем о себе очень много. Мы научились различать стимулы, классифицировать их, поэтому мы, как и следовало ожидать, реагируем на стимулы скорее чем на стимулирование. Так мы пришли к совершенно неверному заключению, а именно, что системы могут знать, как отвечать только на те стимулы, о которых они знают заранее и их классифицировать. Конечно, нам возразят, что инженер не может создать машину или конструкцию, защищенную от неизвестности, от непредвиденных помех, но только против тех, которые перечислены ему заранее. Мы должны определить, что считается стабильной работой машины, говорят нам, а затем перечислить по порядку помехи, которые считаются нарушителями стабильности ее работы. Тогда и только тогда мы будем в состоянии создать или запрограммировать систему, которая "правильно" воспримет помеху в ее работе. Все это неверно. То, в чем действительно нуждается система, и это все, в чем она нуждается, так это в способе измерения ее собственной внутренней тенденции отклоняться от стабильного, состояния, а также в наборе правил проведения экспериментальной проверки ее реакций, которые приводят ее обратно к внутреннему равновесию. Следовательно нет нужды знать наперед, что вызовет нарушение работы системы, как нет нужды знать, что ее нарушило. Получить уверенность в том, что что-то случилось, классифицировать это нарушение и быть в состоянии изменить внутреннее состояние так, чтобы нарушение исчезло - вполне достаточно.

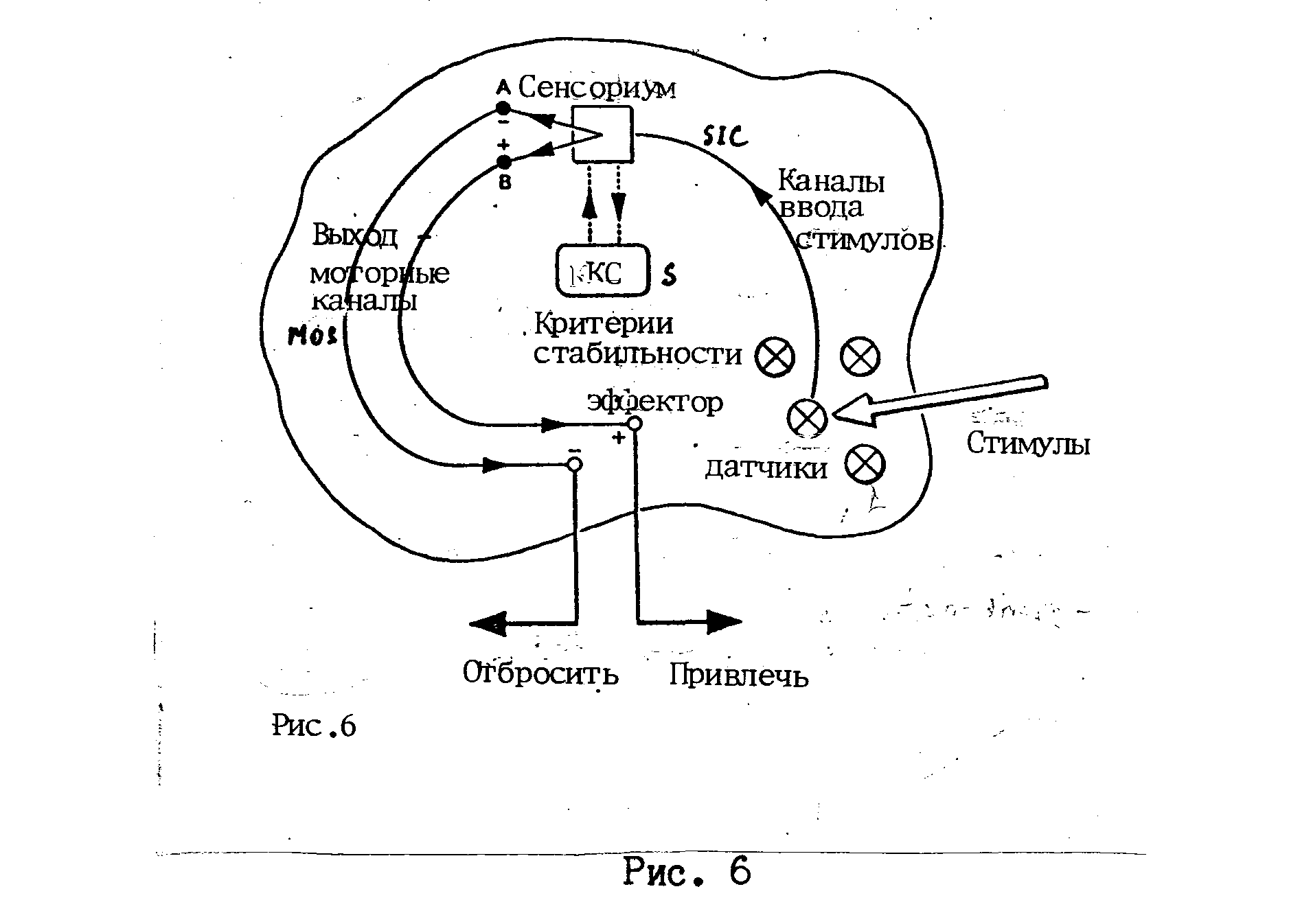
Система, которая может это сделать, которая может справиться со случайным и непредвиденным вмешательством, известна в кибернетике как ультрастабильная система (по номенклатуре Эшби). Например, можно представить себе устойчиво работающий компьютер, который в случае пожара в здании, будет продолжать щелкать цифры, даже когда начнут плавиться его части. Можно подумать, что для защиты от подобного риска конструктор должен установить температурные датчики. Ничего подобного. Любой ультраустойчивый компьютер должен обнаруживать не пожар (обходиться без термометров), а "нарушение работы", поскольку внутреннее контрольное устройство должно показать, что счет стал неверен. Компьютеру тогда следовало бы привести в движение свои колеса и просто покинуть горящее здание. В таком случае люди могут подумать, что компьютер в состоянии "почуять пожар" и снова они ошибутся. Разумное поведение часто основывается на простых механизмах, вроде только что упомянутого, которые вводят нас в заблуждение, заставляя думать, что они основаны на более глубоком понимании обстоятельств. Простейшая версия управляющего устройства, управляющей функции системы, которую можно себе представить, выглядит тогда как, как показано на рисунке 6.

Сенсорное устройство - sensorium - прямоугольник на рис. 6, входящее в систему, может регистрировать наличие стимулов и классифицировать их. Контрольное устройство в нем должно либо усиливать /+/ либо уменьшать /-/ действие стимулов, в зависимости от того помогают или нарушают они деятельность системы в целом. Для этого они включают и заставляют срабатывать точки А или В, которые далее предпринимают действия в зависимости от характера стимулов. Чтобы выбрать между А или В, контрольное устройство должно сравнить ожидаемый результат эффекта своего выбора по критерию стабильности системы (с или S ). Чтобы сделать это, его простейшая стратегия состоит в том, чтобы двинуться немного в сторону уменьшения, а затем немного сторону усиления стимула, сопоставить получаемые результаты по своим критериям и затем твердо установить переключатель. Если система будет экспериментировать слишком долго, то она начнет раскачиваться. В технике это называется рысканием, в психологии - атаксией. Все системы подвержены этой болезни. Если таково простейшее устройство управления, то теперь следует убедиться в том, что мы достаточно глубоко понимаем это и овладеть основной терминологией, необходимой для ее изучения.

Стимулы, как было показано, возникают вне системы. Стимул может возникнуть и по внутренним причинам, но наше утверждение сохраняет силу - должно быть устройство, регистрирующее что что-то произошло и переводить происшедшее, каким бы оно ни было, в термины, имеющие смысл для управляющего устройства. Такое устройство есть часть системы - оно не является стимулом, а тем, что его обнаруживает. Оно называется трансдюсером (датчиком), то есть таким устройством, которое следит за стимулами для всей системы - оно помечено на рис. 6 крестом. В систему вероятно входит один сенсориум (одно сенсорное устройство) но, конечно много трансдюсеров. Фактически, основная классификация стимулов происходит в самом начале и сводится к тому, чтобы разобраться какой из трансдюсеров стимулировался.

Когда трансдюсер сработал, сообщение о стимуле поступило в систему. Канал, по которому сообщение о стимулах поступает в систему - черная жирная линия SIС (рис. 6), называется сенсорным каналом ввода. Эти сообщения являются сенсорными входными данными. Другая половина цепи управления, ее замыкающая, является моторным каналом выхода (МОС). Соответствующий "мотор" связан с выходом, потому что выходные данные имеют смысл постольку, поскольку выход вызывает действия. Например, в психологии, нервы, связывающие выходные каналы, как говорят, передают эффективные импульсы (которые могут быть стимулирующими либо ингибиторными /подавляющими/ или + или -), тогда как сенсорный ввод является "аффекторным". Таким образом моторный выход ведет к эффектам (пустая цепь на рис. 6), способными действовать в зависимости от стимулов. В простом случае один из них побуждает систему действовать в пользу стимулов, другой - избавляться от них. Тогда, заметьте пожалуйста, системе безразлично, что собственно вмешивается в нее.

Действующие в реальной жизни системы управления, конечно , много богаче; масса импульсов пробегает через огромное число входных и выходных каналов. Это справедливо как в отношении тела человека, так и в отношении управленческих ситуаций. Этот факт не меняет базовой структуры сенсорных и моторных узлов в цепи управления; мы, однако, должны принимать во внимание, при рассмотрении операций переключения, которые подготавливают решения, что в больших, комплексных системах этот процесс никогда не бывает столь простым переключением, как на нашей схеме (рис. 6).

В частном случае управления техническими средствами такая процедура переключения вполне понятна. Закономерность, показывающая как она работает, известна как функция преобразования, поскольку она математически указывает, какого сорта преобразования происходят между сенсорными и моторными узлами в цепи управления. Математическая форма функции преобразования является дифференциальным уравнением и может быть весьма сложной. Сложность возникает потому, что характер реакции системы часто определяется диапазоном стимулирования, вызванного данным стимулом или частотой, с которой происходит стимулирование. В живых системах управления самым наглядным примером функции преобразования является нейрон или отдельная нервная клетка. Как утверждает Маккуллох, функция преобразования в этом случае будет весьма сложной и описывается нелинейным дифференциальным уравнением восьмого порядка. Мозг человека состоит вероятно из 10 000 000 000 нейронов и насколько мы знаем, нет двух из них, у которых были бы одинаковые функции преобразования. Мы столкнемся с проблемой именно такого порядка при обсуждении функции преобразования руководителя. Решение, принимаемое в бизнесе, может касаться десятка руководителей, но это просто в сравнении с несколькими тысячами нейронов. Но функцию преобразования, управляющую нейронами, совершенно невозможно составить - если бы в этом было дело, - поскольку она есть некоторая сумма взаимодействующих нейронов мозга.

Дальнейшее еще сложней. При рассмотрении управления системой в целом, что является нашей конечной целью, мы вполне можем столкнуться с тем, что нам не удастся даже опознать отдельные входные и выходные каналы, а только целые связки их. Еще меньше наши возможности идентифицировать индивидуальные переключатели, преобразующие функции которых по этой причине не могут быть исследованы и еще менее измерены. Тому есть существенные структурные причины, которые обнаруживаются в психологических структурах, таких как нервная система, и в социальных структурах, таких как корпорации и фирмы. В подобных случаях сенсорные входные данные поступают в сенсори-ум распределение, а триггеры моторных действий тоже распределены широко и не просто по всей периферии системы, а не только между точками А и В, о которых мы упомянули. Проблема переключения следовательно охватывает весь набор входящих и весь набор выходящих импульсов. Вместо одного переключателя между ними мы, следовательно, получаем сложную соединительную сеть. Такая сеть называется по-латыни reticulum кибернетический вариант называется anastomic . Этим мы хотим сослаться на тот факт, что множество ветвей такой сети целесообразно взаимодействует, но невозможно разобраться в том, как сигнал поступает в ретикулум. Этот термин просто означает, что каналы ввода заканчиваются как дельта реки множество потоков вливается в море и такие потоки кроме того, часто переплетаются один с другим. Нет никакой возможности проследить каким путем данная пригоршня воды попала в море, как нет способа указать на то, из какого протока или источника она туда поступила.

Весьма важно усвоить это замечание об анастомотик ретикулум, поскольку процесс принятия решения как в теле человека, так и сообществе руководителей работает именно так. Мы видим информацию, которая была получена, видим предпринятые действия, эффекторные и аффекторные каналы, через которые эти меры осуществлялись и только.

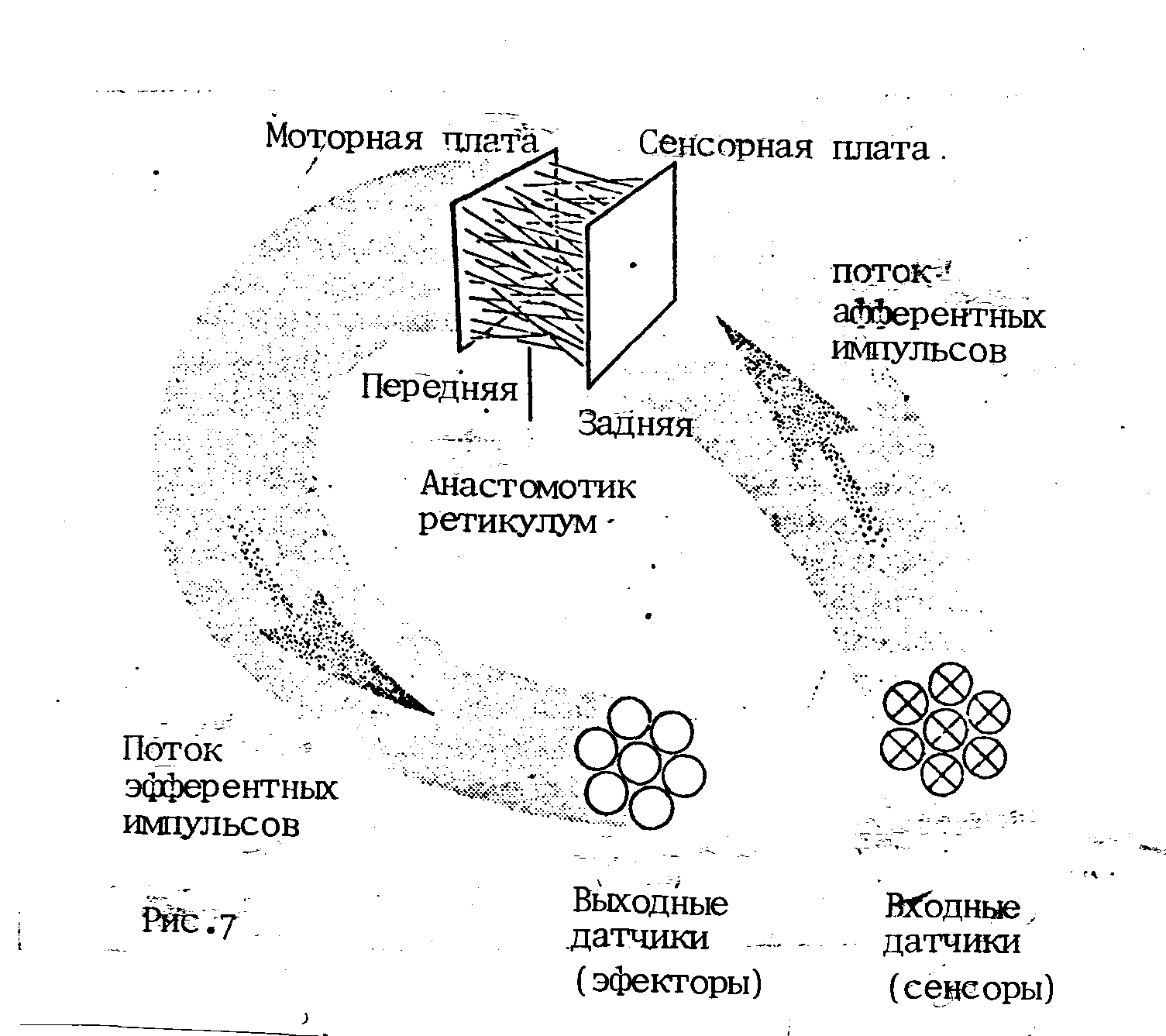
В этих условиях разумно перейти к электрической модели и попытаться представить и изобрести систему переключателей действующих на скрытые от глаз цели принятия решений. Более того, при рассмотрении рис. 6 казалось разумной рассматривать эти соединения как переключатель (А. или В) на нашем рисунке. Так можно было поступить, поскольку мы рассматривали простейший случай. Без сомнения бывают простые случаи и в управлении - когда управляющий говоря по телефону, скажет взять курс А или В - он принял решение и положит трубку. В подобных случаях функция преобразования может быть выражена в терминах минимизации стоимости решения. Но это тривиальный случай. Нормально, также трудно сказать, какие внутренние причины повлияли на группу руководителей, принимающих решение, как проследить путь воды в дельте реки. Поэтому, чтобы сделать модель более реальной, мы должны теперь модифицировать главную цепи (рис. 6) и представить ее как показано на нижеследующем рисунке 7.

Применительно к этому новому варианту модели важно подчеркнуть следующее: стимулы возбуждают целую колонию трансдюсеров входа или сенсоров, а реакция системы осуществляется через целую колонию выходных трансдюсеров или эффекторов. Оба эти набора трансдюсеров служат передатчиками импульсов, используя множество каналов. Сенсориум и связанный с ним переключатель заменены своего рода коробкой, имеющей сенсорную панель сзади и моторную панель спереди. Эти панели соединены своеобразной сетью переключающей системы, которую мы назвали анастомотик ретикулум.

Все сказанное в этой главе до сих пор касалось управления большими комплексными системами, исходя из первых npинципов, а все введенные нами термины были с сильным биологическим акцентом. Был упомянут также инженер-автоматчик, но в основном с тем, чтобы сказать, что ему трудно чем-то помочь нам! Однако теперь он снова выступает на авансцену, чтобы ввести новый термин - важнейшую концепцию из всех -

обратную связь. Прежде всего заметим, что было бы ошибкой принять связь между стимулом и ответной реакцией за систему обратной связи. Этот термин стал настолько вольно использоваться в ряде мест, что почти всякая реакция на любое действие принимается за обратную связь. Содержание этого термина следует вскрыть с известной осторожностью, поскольку он относится к фундаментальным понятиям кибернетики. Для его объяснения нам придется ввести немного математики, в самой общей форме, в надежде, что ее использование приведет к правильному пониманию термина даже читателем - не математиком.

В системе есть вход и есть выход. То, что происходит внутри системы и превращает первое во второе уже было названо функцией преобразования. В технике управления, как говорилось, такая функция описывается дифференциальным уравнением - оно определяет скорость преобразования ввода в выход во времени. Оператор в этом преобразовании обычно обозначается буквой "р". Нам нет необходимости входить в типичные детали этого уравнения, достаточно упомянуть, что оно в общем является функцией оператора "р". Как говорилось ранее, функция преобразования нейрона может быть достаточно хорошо описана нелинейным дифференциальным уравнением восьмого порядка, однако ее тоже можно записать как f.p) . Беда в том, конечно, что хотя мы можем ее так записать, мы в действительности ее не знаем. Трудность здесь точно такая же как в заявлении "пусть x - есть число жителей в данном городе". Далее мы свободно пользуемся x в наших расчетах и возможно могло бы посчитать число семей в городе, как функцию от х но рано или поздно нам придется узнавать, что стоит за числом х.

В технике управления существуют методы точного определения дифференциального уравнения для данного f(p) . Прежде всего оно превращает ввод в выход. Это означает, что мы можем определить f(p)=o/i, где i - временное значение входа и о - переменная величина выхода. Когда дело идет о цепях управления, с которыми имеют дело инженеры-автоматчики - ввод и вывод поддаются непосредственному измерению. Более того, если можно построить график выхода в зависимости от входа во всем диапазоне их изменений, то можно с уверенностью считать наличие зависимости между ними. Функция преобразования и есть уравнение, описывающее такую зависимость. Она может быть очень сложной, но ее можно найти, особенно потому, что мы обычно располагаем множеством доступной нам информации относительно переключателей и цепей, из которых состоит изучаемая нами система. Знание структуры системы позволяет математикам предсказывать вид требуемого в данном случае уравнения. Найти значение f(p) в типичной кибернетической ситуации может оказаться невозможным. Как мы уже видели, трудно и отчасти может быть лишено смысла принимать что-то за вход или за выход в психологических, социальных и управленческих ситуациях. Может оказаться невозможным выделить, не говоря уже - измерить , интересующие нас переменные. Тогда нам никак не удастся получить зависимость переменных на выходе от переменных на входе. А если структура цепи, как говорилось, представляет собой анастомотик ретикулум, то трудно сформировать какую-либо математическую гипотезу относительно формы соответствующей данному случаю функции преобразования.

Однако мы должны теперь вернуться к инженеру-автоматчику и его сервомеханизму как называется его прибор управления. Инженер знает вход, выход и функцию преобразования для своей системы. Стоящая перед ним задача сводится к следующему: выходной результат системы может не полностью соответствовать тому, который ему нужен. Предположим, например, что при устойчивом входе функция преобразования дает устойчивый выход, который точно соответствует желаемому. Теперь пусть вход начнет регулярно изменяться - что произойдет с выходом? Он может следовать за входом, поскольку предполагалось, что он постоянен. Хуже того, он может усиливать колебания на входе и дать сильнне раскачивание, опасное для следующей системы, для которой выход данной системы является ее входом. Что бы не случилось, во всяком случае, можно измерить текущие изменения значений переменной на выходе и сравнить их с ожидаемыми. Полученные при таком измерении результаты выявят отклонения системы от нормы. Именно такие измерения, которые также могут быть подвергнуты некоторой модификации, подаются обратно с целью отрегулировать вход так, чтобы существующая функция преобразования определила правильный выход.

Представим себе такой простой цифровой пример - пусть функция преобразования удваивает величину входа. Пусть в данный момент значение входа равно 3, тогда на выходе будет 6 , а 6 и есть то, что нам нужно. Представим теперь, что по неизвестной нам заранее причине значение выхода внезапно стало равным 8. Тогда отклонение на 2 будет воспринято как значение выхода, это означает, что значение входа по той или иной причине стало по своему эффекту равно 4. Цепь обратной связи воспримет как свой вход отклонение выхода на 2 единицы и теперь должна сработать при таком его значении. Если она просто направит обратно отклонение в 2 единицы как поправку на вход в систему, то теперь при его, как мы помним, значении равном 4 на входе останется только 2. Функция преобразования его удвоит и новое значение выхода станет равным 4 вместо 6. Ясно, что цепь обратной связи нуждается в своей собственной функции преобразования, которая снизит первичное отклонение выхода с 2 до одной единицы и заставит первичное отклонение входа снизиться на это значение. Тогда выход системы возвратится к требуемой 6, поскольку ввод теперь исправлен на 3.

Этот пример хорошо демонстрирует механизм действия отрицательной обратной связи, исправляющей ошибку, но он с дефектом. Мы заморозили систему, чтобы рассмотреть фактические показатели, а затем позволили ей работать снова на конечном интервале времени, необходимом для срабатывания обратной связи. Однако причиной всех неприятностей является неожиданное изменение величины сигнала ввода и, вероятнее всего, он изменится снова ко времени проведения корректирующих действий. Тогда то, что произойдет за время отклонения и введения в систему обратной связи, сложнее, чем просто изменение на обратное значение первичной функции преобразования. Если бы это была единичная операция, то легко было бы видеть, что систематическое изменение входа, которое происходит в фазе с временным циклом обратной связи, не будет заглушено, а возрастет. Наш механизм обратной связи обнаружит первичное отклонение +2 и снижение входа на единицу последует точно в момент, когда вход даст импульс, приводящий его в результате к отклонению на -2. Иначе говоря, на входе останется эффективно 2, что генерирует 4 скорее, чем 6. Тут вступит в строй обратная связь, считывающая первое (позитивное) отклонение и снизит его с 2 до I. Теперь на выходе останется 2 вместо б, что еще хуже.

Из этого следует, что обратная связь должна иметь свою собственную функцию преобразования, которая может быть записана как F(р) и она должна быть умно сконструирована, чтобы производить подавляющий эффект, скорее чем усиление флуктуаций на входе. Допустим, что так или иначе это может быть сделано и мы получили тот впечатляющий результат, которого мы добиваемся - саморегулирующий механизм, действующий иcходя не из понимания причины нарушения, а исходя из производимого им эффекта. Дело в том, что причиной отклонения может быть изменение температуры (а система не сделана так, чтобы это обнаруживать), или нарушение соединения (которое не предполагалось) или отказ в другой системе, генерирующей вход для данной системы о которой система ничего не знает). Важно для нас, чтобы управление осуществлялось независимо от причины нарушения.

Чтобы уяснить разницу между первичной функцией преобразования -f-(p) и нововведенной F (p) , мы должны сослаться на первую сеть и сеть обратной связи - которые управляются этими двумя функциями соответственно. "Сеть" по-прежнему подходящий для нас термин, поскольку реальные системы значительно сложнее, чем простые из числа рассмотренных нами

здесь, где все можно разглядеть в виде единичных линий и петель. "Сеть" на простом русском языке звучит лучше чем латинское "ретикулум", как упоминалось ранее, поскольку мы теперь создаем систему со специальными соединениями. К названию ретикулум мы будем прибегать чтобы ссылаться на общие и возможно не специальные случаи внутренних соединений в том контексте, в каком это слово первоначально было введено.

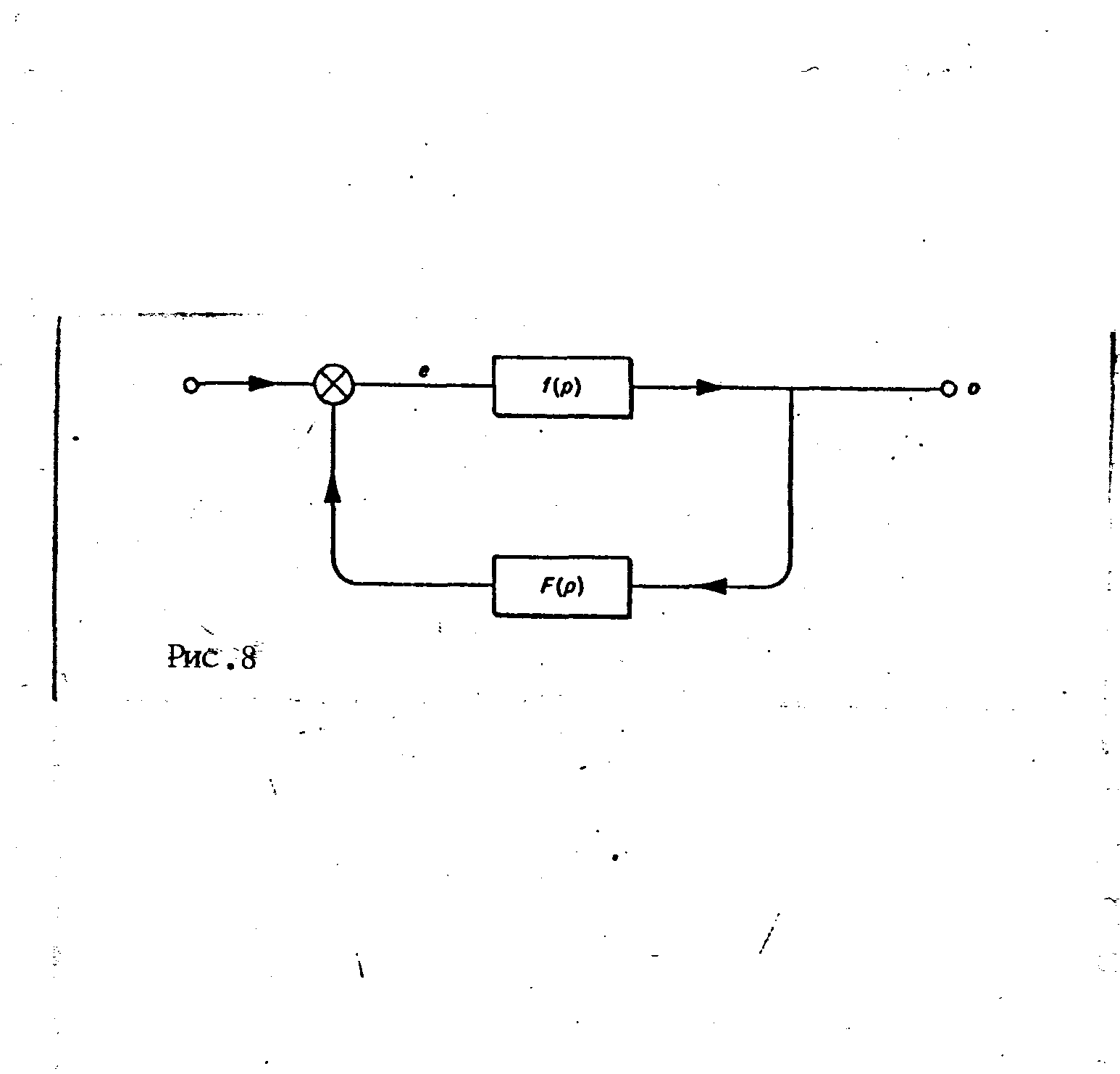
Теперь посмотрим на схему простого сервомеханизма (р. 8) - нам предстоит исследовать характеристики обратной связи, исходя из его математической формы. Это не означает, что мы будем изучать конкретные дифференциальные уравнения - вся дискуссия ограничитcя элементарными алгебраическими уравнениями, но это надо преодолеть.

Вход в систему обратной связи есть выход предыдущей системы б. Выход системы обратной связи есть модификация ее значения, после того как на нее воздействует функция преобразования системы обратной связи, что можно записать как: o f(p) . Вход в предыдущую систему, который был сначала равен С , станет теперь равный 6 после приложения к ней обратной связи. Тогда можно считать:

e = i+o- o.F (p)

Если это так, то форма функции преобразования первичной системы изменится. Первоначально мы ее записали как f(p)=o/i, но теперь это не годится. Выход первой системы (изображенный в прямоугольнике как f (р) теперь уже не i , а е представляющей комбинированный эффект входа i и обратной связи о F(p) . Поскольку f(p) восприняло е и дало выход o , запишем тогда f(p)⁼ o/e , Чтобы получить функцию преобразования всей системы, мы должны вернуться к основному определению, в котором сравнивался выход со входом и записать новую функцию Ф (р) , которая ставит обе функции f(р) и F(p) в правильное соотношение. Конечно просто записать Ф(р)=o/i. Но чтобы сделать то, что нам нужно, перепишем уравнение для первой системы f(p)=o/i и уравнение для е . Тогда получим:

Ф(p)=o/i=f(p)/1-f(p)F(p)

Несколько заключений следуют из рассмотрения этого уравнения. Во-первых, видно как обратная связь может стать либо положительной либо отрицательной.

Рассмотрим условия перемножения функций обратной связи первичной цепи и цепи обратной связи, а именно: f(p)F(p)

Предположим, что система не требует коррекции, т.е. функция обратной связи не оказывает никакого влияния. Тогда перемножение функций даст нуль и общая функция преобразования Ф(р) будет правильно работать как f(p) сама по себе. Если перемножение функций будет больше нуля, то знаменатель станет меньше единицы, а общее значение функции больше, чем значение функции преобразования первичной цепи - в итоге получится положительная обратная связь. Если перемножение функций станет больше нуля, то знаменатель станет больше единицы и значение результирующей функции станет меньше значения функции преобразования первичной цепи - получим отрицательную обратную связь. Очевидно, что одна и та же система может дать как позитивную-положительную-обратную связь, так и отрицательную, в зависимости от формы переменной, действующей на входе и сдвига по фазе во взаимодействии этих двух цепей.

Во-вторых, весьма интересен результат действия отрицательной обратной связи. Корректирующая обратная связь по необходимости должна быть отрицательной, если любое отклонение от заданной нормы считается по его абсолютному значению положительным. Тогда уравнение для е должно быть переписано, как e = i - o F(р), поскольку нам известно, что абсолютное значение функции преобразования ошибки должна вычитаться из первичного значения входа. Тогда следует переписать уравнение для общей функции преобразования и записать его как:

Ф(р) = f(p) 1+ f(p)F(p)

Анализируя это уравнение, можно заметить, что произойдет, если функция преобразования первичной цепи станет очень большой величиной. Постольку-поскольку значение f(р) существенно больше значения общей функции, то значимость 1 теряется и

тогда f(p) можно сократить. В таком случае функция преобразования в сети обратной связи станет предопределяющей для общей функции преобразования. Запишем формально:

если |f(p)| >>1, то Ф (p) = 1/ F(p)

Результат удивителен. У нас может быть очень слабый сигнал на входе, как это часто случается в биологических и управляющих ситуациях. Мы можем сильно усиливать этот сигнал в первичной цепи и это часто случается. Тогда можно предположить, что любой "шум" на входе, то есть по смыслу, любая неверная информация на входе, станет также сильно усиливаться. Но поскольку над системой в целом доминирует не первичная цепь, не первичная система, а система обратной связи, то именно она обеспечит, что выходной сигнал станет значительно чище, чем можно было ожидать.

Таким образом мы оказываемся на пути к достижению желаемого качества системы - ее ультрастабильности. Отрицательная обратная связь корректирует выход в соответствии с флуктуациями на входе во всех случаях. Неважно какого сорта шум действует на систему, как он велик по сравнению с входящим сигналом, насколько он хаотичен и почему возник. Система стремится уничтожить его влияние.