Глава 3 РАЗМЕР ПРОБЛЕМЫ

„ Как было показано, всякая система управления состоит из трех частей: устройства входа, устройства выхода и сети связи, которая соединяет их, Эта сеть в самом общем случае является анастомотик ретикулум. Теперь попытаемся найти численное выражение, которое количественно характеризующее, такую систему. Многое можно сказать о размерах проблемы исходя из уже перечисленных первых принципов.

Прежде всего должен быть организован вход, начиная с набора рецепторов, которые передают информацию о некоторых аспектах состояния внешнего мира в эффективно действующие каналы, и кончая сенсорным регистратором (или сенсориумом) в котором эта информация накапливается. Принципиально такое сенсорное устройство можно встретить везде, как в живых так и в искусственно созданные системах. Телефония использует различные способы вибрации диафрагмы в телефонной трубке в качестве набора рецепторов, с помощью которых голос направляется в канал входа в телефонный провод. Диафрагма на другом —— слуховом конце трубки принимает колебания, переданные по каналу связи и работает как сенсорное устройство. Несколько по другому работает телевидение, здесь передающим каналом служит не провод, а радиоизлучение. Но и здесь сканирующая система телекамеры представляет собой набор рецепторов, передающих изображение, которое собирается вместе на внешней поверхности телевизионной трубки,которая представляющей собой хороший пример сенсорного регистратора-сенсориума.

Совершенно очевидно, что способности различать детали на каждом конце входного устройства (рецепторы или сенсориум) должны быть равными для обеспечения эффектиной работы системы. Так, если сенсориум обладает большей возможностью различать детали, чем рецептор, эта его способность будет потеряна, поскольку передающее устройство будет генерировать больше сигналов, а приниматься будет лишь их часть. Если же наоборот, рецептор будет более мощным в смысле различения деталей и эта детальная информация будет передана сенсориуму о худшей разрешающей способностью, то некоторые детали будут просто утрачены. Другое очевидное заключение сводится к тому, что емкость любых каналов, используемых для передачи информации между рецепторами и сенсориумом должна быть достаточной, чтобы передать её всю. Это особенно ясно, когда передающий канал - механический.

Возмем, к примеру пишущую машинку в качестве входного устройства системы (Её можно рассматривать в качестве самостоятельной системы, поскольку то, что считатетоя системой, определяется исследователем и он определяет её границы, исходя из своих целей). Клавиши пишущей машинки представляют собой рецепторы с мощностью, скажем, 92 различных символа. Тогда у нас будет 46 клавиш и устройство, позволяющее работать на двух регистрах. Клавиши сделаны для того, чтобы машинистка могла ввести текст в систему, которая собирает его на сенсориуме-бумаге. Если у нас 46 клавиш, то должно быть 46 рычагов, способных перенести металлические символы на бумагу и устройство для переключения регистра, выступающее в виде своеобразного усилителя, поскольку с его помошью удваивается число символов (сколько бы их ни было) представленное числом клавиш. Важно также, чтобы канал передачи обладал соответствующей емкостью, не только в смысле способности различать сигналы, но и в смысле скорости действия. Опытная машинистка, пытающаяся использовать старую машинку, столкнется с тем, что рычаги, несущие знаки не достаточно быстро сменяются, в результате чего два из них могут сцепиться, мешать друг другу.

Но то, что справедливо в отношение ввода, справедливо и в отношении выхода-второго компонента любой системы управления. Возьмем моторную плату, которая передает инструкции набору эффекторов, и здесь мы снова столкнемся с тем, что нет смысла располагать большей емкостью различения на одном конце, чем на другом. Какими бы не были наши порывы действовать, но если их нельзя ни передать дальше по имеющимся каналам, ни превратить затем в соответствующие действия - они бесполезны в любом случае. Если кто-то пытается кричать яхтсмену, испытывающему трудности при входе в гавань, полезные советы, которые сносятся ветром, то это бессмысленно - у него нет эффективного канала связи. Опытный музыкант, играющий партитуру Шопеновского этюда на рояле. прекрасно знает какую клавишу нажимать, поскольку он обладает обычным человеческим телом и располагает достаточной емкостью каналов, чтобы преобразовать требуемую ноту в движение мускулов. Но если человек никогда не учился игре на рояле, то он бессилен произвести требуемые действия. Он не обладает дффекторами (выходными датчиками).

Третья часть системы управления - анастомотик ретикулум, который соединяет сенсоры с моторной платой. О нем нам еще предстоит подробней поговорить. А сейчас попытаемся оценить масштаб проблемы, перед которой стоит система управления любой сложной организацией, такой как человек или промышленная фирма, в терминах входа и выхода. И уж поскольку оба эти термина снова сказаны вместе, отметим один любопытный факт. Мы говорили о способности частей системы управления различать детали. На стороне входа необходима емкость равная набору рецепторов на сенсорной плате; на стороне выхода должно быть такое же положение на моторной плате ее эффекторов для действия. Рассматривая систему управления в целом, мы видим, что необходимая мощность как на входе, так и на выходе должна быть равной. Основания для этого все те же, если мы по прежнему исходим из посылки, что критерием является эффективность системы. О6ычный случай, когда (например) качество каналов передачи информации ухудшается из-за их физических свойств и информация будет искажаться - должен рассматриваться по-другому. В таком случае нам потребуется большее количество входных данных, чем действительно необходимо, а избыток будет использован для компенсации ухудшения каналов связи. Например, если посыльный, которого мы направляем с письмом по дороге будет убит с вероятностью 50%, то мы обязаны посылать двух человек с письмом одинакового содержания - хотя, конечно, только одно письмо необходимо на другом конце.

В кибернетике, число различаемых объектов (или различаемых состояний того же объекта) называется "разнообразием". Тогда, подводя итог вышесказанному, можно считать, что разнообразие на входе должно (по крайней мере) соответствовать разнообразие на выходе для системы целом, но для устройства входа и устройства выхода решается самостоятельно. Это существенно важное следствие закона Эшби о разнообразии систем, которое гласит, что управление может быть обеспечено только в случав, если разнообразие средств управляющего (в данном случае всей системы управления) по крайней мере не меньше, чем разнообразие контролируемой им ситуации. Этот закон, как и любой другой важный закон природы, совершенно очевиден - после того как он открыт. Нетрудно, однако, обнаружить примеры систем управления, которые не соответствую этому закону довольно сильно и следовательно, неудовлетворительных. Начиная с управления уличным движением и кончая национальной экономикой - ошибки очевидны и, конечно, это одна из ключевых проблем управления промышленным предприятием. Руководители всегда надеются создать простую и дешевую систему управления, но часто заканчивают потерей крупных денежных сумм, на то, чтобы с запозданием обеспечить требуемое разнообразие, которое должно было бы создаваться прежде всего.

Важнее всего определить размер разноообразия промышленного предприятия. Чтобы понять в чем тут дело, мы постепенно подойдем к пониманию того как растет разнообразие и каким путем оно может быть воспринято т.е. к тому, что собственно и есть управление. Рассмотрим для начала проблему чтения в терминах её основной компоненты - распознавания букв. Мы хотим получить возможность различать 26 букв английского алфавита, оставляя в стороне такие сложности как заглавные и прописные, тип шрифта и тому подобное. Представим тогда себе 26 различных карточек, на каждой из которых напечатана одна буква алфавитами создадим рецептор, который их рассматривает по отдельности.

Пусть единичный визуальный рецептор простое устройство, отличающее светлое от темного. Им может быть, например, фотоэлемент, который можно отрегулировать так, чтобы он чувствовал рубеж между светлым и темным. Фотоэлемент таким образом будет обладать двумя положениями, которые мы назовем 0 и I. Если такой единичный рецептор увидит карточку о буквой А и зарегистрирует меру её серости, как определенную смесь черного и белого на этой карточке. Он не увидит формы, которой для нас соответствует буква А, а увидит нечто уникальное в букве А из серии наших карточек. Далее,буква В может дать другую смесь белого и черного, другую градацию серости. Поскольку мы можем изменять порог чувствительности фото элемента, чтобы он регистрировал либо 0 либо 1,ио появляетоя возможность менять порог его чувствительности (по крайней мере теоретически) так, чтобы он отличал букву А от В. Когда ж мы дойдем до С, то разнообразие нашего фотоэлемента увы уже исчерпано, т.е. мы уже ничего не можем сделать с последующими буквами от С до Z. Ясно, что одного рецептора недостаточно. Более того, как кажется нам нужно 26 рецепторов, каждый тщательно отрегулированный на свою букву. Если это так, тогда мы удовлетворим закон о требуемом разнообразии: число, фотоэлементов, присоедиенных к рецепторам входа и сенсориуму станет соответствовать 26 состояниям, paссматриваемого нами любого слова. Однако, если у нас есть только один оригинальный рецептор, мы можем проделать о ним трюк другого сорта. Можно разделить весь набор карточек с буквами на две части, так чтобы в одной половине оказались более светлые, а в другой более темные буквы. (При этом предполагается, что можно создать такой шрифт, когда у каждой буквы будет свое особое соотношение черного и белого).Такая их организация позволит относить карточку только к одной из двух групп, поскольку такова возможность рецептора оценивать разнообразие. Но этот элемент будет обследовать все карточки рассортировывать их на две пачки - на более светлые (которые рецептор принимает за 0) и более темные (которые считаются за I). Если мы достаточно точно установим границу чувствительности, то в каждой пачке у нас будет по 13 карточек. Рецептор таким образом в состоянии считывать все 26 карточек и дать 26 сигналов, один за другим, как серию нулей и единиц и распределять каждую карточку в соответствующую пачку.

Преимущество всего этого в том, что здесь один рецептор с разнообразием два (а именно 0 или I) способен уменьшить в два раза решение проблемы соотнесения любой из 26 букв. Мы таким образом получили 13 разнообразий за счет двух. Может показаться, что пользы в этом мало, однако это весьма важно.Вообще, бинарный классификатор (рецептор 0 или I)сокращает в два раза неопределенность,с которой он встретился, если он эффективно использован. Все проблемы, относятся ли они к распознованию или класификации или к самому решению проблемы неопределенности. Если нет неопределенности в отношение промышленной ситуации, то руководителю не нужно принимать решения. Если нет неопределённости в том, какая это буква, то мы можем её прочесть. Ситуациями с большой неопределенностью трудно управлять именно потому, что тут разнообразие и есть мера их неопределенности.

Именно поэтому так важен трюк, который мы только что продемонстрировали. Как бы не была велика проблема, ее разнообразие, в принципе, может быть уменьшено в два раза используя один, решающий элемент. Приведем другой пример. Вы ищите кого-то в танцевальном зале, где танцуют 500 пар. Разнообразие тогда составляет 1000; фактор неопределенности составляет. 1:1000, а вероятность правильного её решения равно 0,001, при случайной выборке. Таков масштаб проблемы. Но если вы знаете ищете ли вы мужчину или женщину, то проблема сразу же сокращается в два раза.

Вернемся теперь к проблеме чтения всего алфавита, Мы показали, что 13 более светлых букв могут различаться от 13 более темных букв с помощью одного дискримнационного рецептора, способного определить среднюю границу их серости. Взяв тепеpь пачку карточек из 13 букв и второй рецептор мы получим возможность отделить 6 одних букв от 7 других, используя такое же устройство-фото элемент, порог чувствительности которого был бы на средине между самыми темными и самыми светлыми буквами. Конечно, такой же рецептор можно использовать для сортировки второй пачки букв, когда очередь до них дойдет. Третий рецептор используем для сортировки шести или семи) карточек, который сведет проблему к двум новым половинам (из 3 и 4 карточек). С четвертым рецептором мы сможем разобраться и о этими пачками, поскольку знаем, что каждая буква уже проверена и является одной из двух букв. Тогда пятый рецептор различит и эти оставшиеся две буквы. Неопределенность, с которой мы начали определять любую 26 букв, теперь исчезла - мы теперь знаем какая буква какая и достигнуто это использованием пяти фотоэлементов.

Таким образом в принципе необходимы только 5 рецепторов, чтобы прочесть буквы английского алфавите, поскольку их достаточно, чтобы различать

2⁵=32 буквы, полагая, что у каждой буквы свое соотношение белого и черного, своя мера серости, которая уникальна. В общем n является минимальным числом рецепторов, способных различать 2ⁿ возможностей. Заметьте, что таким образом получается впечатляющая экономия числа рецепторов по мере увеличения числа возможностей. Десять рецепторов могут различать 2¹⁰ 1024 буквы или чего-то другого. Сорок рецепторов смогут различить 2⁴⁰ - что больше миллиона миллионов. Такое число - чистая теория, поскольку мы должны заметить, что на практике такое множество букв (или состояний, или картин нашего мира) не может быть точно различимым. Частично, так происходит поскольку пороги различия их серости становятся слишком близкими друг к другу, чтобы использовать практически полезный инструмент для их различения, а частично из-за того, что буквы невозможно напечатать с такой аккуратностью. Другими словами, нечеткость их контуров дает такую меру аккуратности для одной буквы, которая точно соответствует тому, что есть у другой, которую нужно от неё отличить. Так мы подошли к проблеме разнообразия в пропускной способности канала связи, как отличающейся от разнообразия входа,

Мы можем начать обсуждения проблемы снижения разнообразия с другого конца. Сканирующая система телевидения располагает сотнями линий и сотни разной яркости черных и белых точек передаются по каждой линии. В конечном счете, чтобы генерировать картинку на трубке должны использоваться десятки тысяч двоичных рецепторов. Подобно этому в каждом человеческом глазу примерно около миллиона двоичных рецепторов. Не удивительно тогда,

что глаз или телевизионная трубка может различать 26 букв алфавита, поскольку, как было показано, для этого достаточно и пяти рецепторов. Из этого вытекает важное заключение: используя значительно большее число рецепторов, чем теоретически необходимо, мы фактически можем разобраться с невероятно большим числом неточностей на входе. Это аналогично нашему примеру о необходимости в двух курьерах для передачи единственного собщения ,хотя на этот раз речь идет о рецепторах, а не о каналах связи. Благодаря этому люди смотрят телевизионные передачи сравнительно спокойно и конечно с пониманием происходящего, когда изображения сильно искажено электрически вехами. Аналогично глаз спокойно читает исключительно плохой почерк. Так происходит потому, что у глаза достаточно рецепторов, чтобы различать миллионы букв, а не каких нибудь 26, но если учесть вое возможные алфавиты, включая буквы написанные от руки, то вероятно, нам нужно большинство этих рецепторов.

Разница между "да" и "нет", между 0 и I является элементом решения. Руководители могут уклониться от ответственности, давая двусмысленные или расплывчатые решения, если захотят, — могут пробормотать что-то, чтобы отмахнуться, но когда дело доходит до серьезного - ответ всегда бинарен. Фактически руководители всегда используют процесс: дихотомической классификации (который только что был нами описан).но используют его совсем не формально. Проблема управления может решаться сотнями возможных способов и руководитель может отказаться, её решать, сказавши только, что по его мнению решение лежит на том, а не на этом конце шкалы возможных решений. Это звучит весьма неопределенно, но фактически, он здесь разделил возможные решения на две группы, которые вполне могут быть неравными, оставляя границу между группами весьма не четкой. Подчиненные будут разбираться в этих группах в течение некоторого времени, производя действия, которые толкают ситуацию в одном направлении, скорее чем в обратном, пытаясь также избежать зоны перекрытия. Но рано или поздно они достигнут такого положения, когда они перестают знать, что делать дальше, но представят руководителю значительно суженый круг возможных решений. Этот процесс будет продолжаться, как успешное разделение спектра возможных решений на все новые половины, пока в один прекрасный день руководитель предстанет перед возможностью сказать да или нет на заключительное предложение. Можно математически показать, что наиболее эффективный путь преодоления последовательных решений такого рода состоит в том, чтобы разделять возможности на две части, причем совершенно неважно, если эти части не равны. Можно, конечно, использовать дополнительный рецептор (что предполагает принятие дополнительного решения) сверх тех, которые минимально необходимы, но это не меняет общего порядка процедуры.

В компьютерах, как всем прекрасно известно, любые сообщения записываются нулями или единицами, в нашем теле также -нервная клетка либо возбуждена для передачи импульса либо нет. В естественных системах, таких как только что упомянутая социальная система управления, или как наше живое тело, граница между 0 и I обычно смазана, вместо того, чтобы быть четко выраженным рубежом. Поэтому необходимо отличать аналоговый счет от цифрового (двоичного). Компьютеры, работающие с пуншированных карт или магнитной ленты, формально двоичны, также как обычные счеты.

Костяшка счетов передвигается либо в одну либо в другую сторону, но не занимает неопределенного положения. Но логарифмическая линейка - аналоговое устройство, поскольку не всегда можно точно сказать на какой цифре вы остановились, - тут есть зона неопределенности. Нервная клетка человека тоже обладает аналоговыми характеристиками, так как никто не уверен совершенно точно в рубеже, когда она даст импульс. Но она получает двоичный импульс, потому что электрические импульсы,идущие по нервам прибывают залпами,интенсивность которых варьируется в смысле частоты их поступления, но не величины их амплитуды. Так, например боль становиться острее вследстивие увеличения числа поступающих по нерву импульсов в единицу времени, а не потому (как думают многие интуитивно),что увеличивается их электрический потенциал. Совершенно также нервная клетка либо посылает импульс - либо нет, но нет вопроса о выдаче ею большого или малого импульса. Но перевод нервной клеткой входящего импульса в выходящий (так сказать её функция преобразования) значительно более трудная проблема.

Большинство систем управления, которые интересуют кибернетиков, представляют собой смесь систем аналогового и дискретного счета. На важность этого утверждения в том, что в любом из этих случаев, мы по прежнему можем измерять разнообразие их состояний в терминах двоичного решения, Неопределенность границ, в конце концов, другого сорта неясность, которая рано или поздно будет решена. Теперь выяснилось, что элементное решение, как выбор между да и нет, между 0 и I является исходным сырьем теории управления. Оно называется бинарной единицей, сокращенно "бит". Мы в дальнейшем будем широко пользоваться этим названием, так, что не ошибитесь, полагая, что биты это понятия, которыми пользуются только специалисты по вычислительной технике и что для всех остальных они интереса не представляют. Измеряя масштабы проблем хорошо использовать при обсуждении их сложности биты как единицу измерения, поскольку они для этого и предназначены. Если ситуация обладает 1024 разнообразными состояниями, то единственное преимущество в знании этого числа состоит в возможности сказать, что нужно принять 10 решений, чтобы рассеять неопределенность, заключенную в этом разнообразии, поскольку 1024 = 2¹⁰. Это просто означает, что мы можем разделять проблему пополам 10 раз, чтобы получить один единственный ответ. Другими словами, бит является мерой экспоненты в нашей формуле 2ⁿ ; он точно равен n.

Такова природа фундаментального механизма, позволяющего нам, как жителям этого мира или как руководителям предприятий справляться о огромным разнообразием о которым мы встречаемся в жизни. Мы можем понять или выбрать или решать среди миллиона миллионов альтернатив используя только 40 хорошо продуманных рецепторов, или классификаторов,или решений. Даже, если мы весьма мало эффективны в разработке своей системы, в планировании её процедур, результат весьма впечатляет. Мы также открыли меру, которую уместно использовать размышляя о проблемах управления и при разработке инструментов управления. Тогда что же произойдет с законом о Требуемом разнообразии? Ответ таков - мы можем создать генератор разнообразия в механизме управления, так же как природа, которая располагает ростом разнообразия как средством преодоления проблем управления.

Пока вcе хорошо, но посмотрим как природа отыгрывается на этом. Если мы? управляющие, можем генерировать очень большие множества из небольшого числа компонент, то тоже может делать и природа. Посмотрите - мы заявляем, что нам необходимо пять рецепторов, чтобы прочесть 26 букв латинского алфавита. Представим себе тогда пять лампочек, которые могут зажигаться в любом порядке.(Первая горит, остальные выключены, две горят - три не горят и т.д.)Тот факт, что 5 рецепторов могут различать 26 букв означает что эти 5 лампочек могут создавать 33 комбинации и конечно, если мы хотим представить себе, что означает наше окружение, то должны понимать то чем оно располагает. Тогда, если внешний мир располагает всего 40 лампочками ,то из предыдущего мы знаем, что можем встретиться с миллионом миллионов разных состояний. Верно, что нам чтобы разобраться в них необходимо всего 40 информационных попыток - ситуация совершенно симметрична. Но мир не состоит из сорока лампочек, а из миллиардов вещей и событий.

Если нас фактически интересует из вещей или событий, каждое из которых в данный момент либо "горит" либо нет, то такой мир предстает перед нами в одном из 2ⁿ возможных состояний вещей. Понимая сколь стремительно нарастает такая функция, перспектива у нас весьма незавидная. Но если мы умеем хорошо создавать управляющие механизмы, то это нас не очень напугает, поскольку это означает необходимость в таком количестве рецепторов сколько насчитывается событий или вещей. Эти и. рецепторов создадут 2ⁿ разнообразий на сенсориуме. Моторная система сведет 2ⁿ состояний к возможным конкретным действиям. Мы таким образом сохранили требуемое разнообразие. Но вспомним ранее приведенный аргумент: если вещей или событий больше, чем рецепторов, которые о них знают и сообщают о них системе управления, то мы не можем определить разнообразия. И здесь мы снова сталкиваемся о законом о требуемом разнообразии. В любой данный момент нас будет касаться лишь то, о чем мы знаем и не больше, а его разнообразие равно n. Из этого n создается 2ⁿ состояний, но наши процедуры выбора позволяют нам с этим справиться, используя n распознаваний или n-выборов, то есть именно с тем их числом, которым мы располагали по определению. Но беда начинается, когда необходимо предпринимать какие-то действия,

Мы уже упоминали, что устройстве входа и выхода симметричны и подчиняются Закону о требуемом разнообразии. Этот аргумент равно распространяется как на вход, так и на выход. Реальная проблема управления, проблема, которую необходимо решать мозгу сводится к проблеме соединения картины

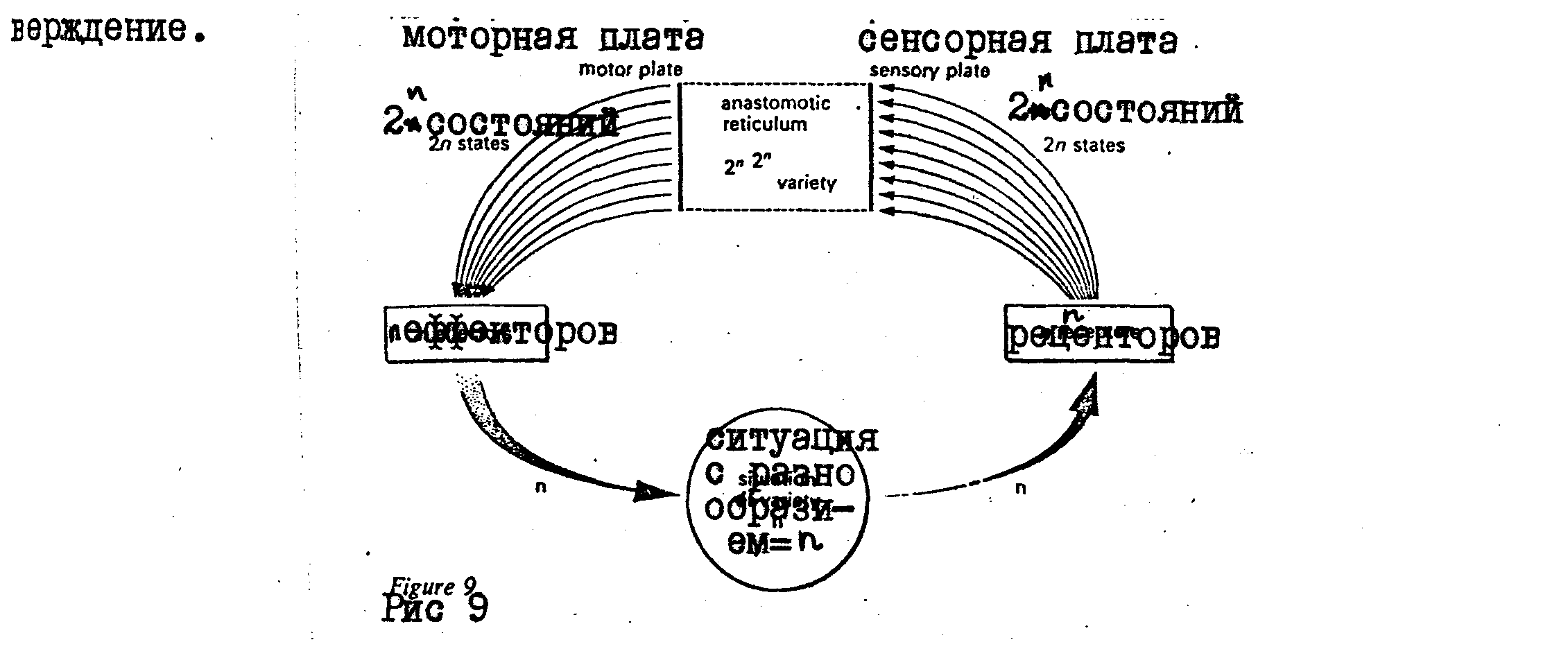
положения на входе о положением на выходе используя анастомотик ветикулум.Еоли разнообразие стоящей перед нами ситуации равно n, разнообразие на cенcориуме равно 2ⁿ если по закону о требуемом разнообразии необходимое число действий составляет n? то разнообразие на моторной плате будет также 2ⁿ.Но каково же тогда разнообразие внутри сети,соединяющей сенсорную и моторную платы? Оно равно числу возможных комбинаций 2ⁿ c 2ⁿ, а это число равно 2ⁿ²ⁿ Рис 9 поясняет это утверждение.

Если мы до этого не намеревались пугаться, то теперь пришло время поднять настоящую тревогу. Дело в том, что числа такого вида немыслимо велики. Следует понимать как это получается. Уже объяснялось почему n разнообразий создают 2ⁿ состояний. Обяснение следовало идя от обратного по мере демонcтрации того как разнообразие разделялось пополам о целью поиска решения. Каждый доступный нам выбор удваивает разнообразие. Начав с единой возможности мы позволяем ей генерировать альтернативу: 0 или I. Если мы повторим эту процедуру, то 0 генерирует либо 0 либо 1, а единица генерирует тоже 0 или I и так далее. Так рассмотрим прямоугольник со всего двумя входами и двумя выходами. На обеих её сторонах-сенсорном и моторном при n=2 генерируется 2ⁿ= 2²= 4 возможности; 00,01,10, 11. Сколько же будет соединений? Ответ таков - разнообразие моторное (4) увеличивает мощность сенсорного разнообразия (4) в 4 раза, а именно в 256 раз.

Как может показаться, в это трудно поверить, поскольку мы начали всего с двух бинарных входов и двух бинарных выходов .Но рассмотрим одно из четырех возможных состоянии выхода, скажем 00. Оно может быть, а может и не быть зарегиcтрированно как одно из четырех выходных состояний.

тояний. Обозначим одно из несостоявшихся соединений 0 ,а действующее I. Нижеследующая таблица демонстрирует возможные состояния системы. В этой системе 16 состояний, вполне различимых, хотя рассматривалось одно выходное состояние. Однако, мы располагаем четырьмя состояниями выхода, в равной мере способных генерировать шестнадцать других состояний внутри системы. Общее взаимодействие входных и выходных состояний дает общееюазнообразие системы - 16 х 16 = 256.Как говорилось, используемая здесь формула 4 ⁴ поскольку каждая из этих четверок есть 2 ⁿ где n = 2,то ясно почему мы ранее записывали наше заключение как 2ⁿ

Почему же нам пришлоcь так подробно в этом раpбираться почему мы заговорили об этом с тревогой? Ответ состоит в том, что любая система управления генерирует столь большое разнообразие, используя этот механизм, что буквально нет никакой возможности его проанализировать и следовательно нет способа (как кажется) соединения для анастомотик ретикулум, "Буквально" - здесь сказано точно - задача кажется научно неразрешимой, не говоря уже о её бесконечно большой размерности. Если это так, то не следует и пытаться или надеяться, что в один прекрасный день появятся достаточно мощные и быстродействующие компьютеры, которые позволят нам претендовать на решение задачу, которую решить нельзя. Факты надо признавать, а они таковы.

Рассмотрим наименьший "мозг", которым стоило бы располагать, чтобы справиться с управлением сложной ситуацией в реальной .жизни любой фирмы. Окружающая её среда характеризуется числом разнообразия её состояний, не так ли? Если представить себя или нашу фирму в окружающей среде, разнообразие которой составляет n=300, что конечно, не так уж и много. Такая оценка весьма консервативна. уж и много.Такая оценка весьма консервативна. У многих фирм больше 300 работающих, более 300 станков, более 300 наименований выпускаемой продукции, более 300 клиентов. Для обстановки с разнообразием всего в ЗОО разнообразие на сенсорной и моторной плате составит 2 ³⁰⁰ — Анаотомотик ретикулум, необходимый для соединения этих плат должен обладать разнообразием 2ⁿ²ⁿ = 2 ^{300 2 300} Измеряя его в битах (поскольку это самая естественная мера для исполъзования в случаях принятия решения) получим 300 х 2 ³⁰⁰ бит, что примерно равно 3х10⁹² бит. Такова мера неопределенности в выбранной нами ситуации-фирме у которой не более 300 входов и 300 выходов, каждый из которых находится всего в двух состояниях.

Следующий аргумент, которым мы обязаны Бреберманну, идет от физики. Как следует из квантовой механики, есть нижний предел точности, с которой может быть измерена энергия. Это означает наличие постоянной и фундаментальной степени неопределенности материи. Любая попытка улучшить точность измерения приводит, согласно принципу Гайзенберга, к тому, что погоня за точностью изменит состояние вещества. Количества здесь малы, но они сильно скажутся на веществе. Бреберманн приложил этот закон к 1 грамму вещества в 1 секунду и показал, что этот нижний предел точности измерения материи определяет верхний предел информационным возможностям материи. Ниже этого предела нули будут приниматься зa единицы и счет станет произвольным. В течение 1 секунды, пишет он 1 грамм типичнoгo вещества не сможет справиться более чем о 2х10 битами информации. Конечно, никто не использовал грамм любого вещества для передачи столь огромного количества данных-микроминиатюризации еще далеко до этого. Но он утверждает, что даже в самом конце технологического прогресса нельзя будет используя 1 грамм вещества передать более 2х10 бит информации в 1 секунду, поскольку они начнут искажаться из-за неопределенности Гейзенберга. Так Бремерманн приложил закон о требуемом разнообразии к самой материи. Такое число выглядит огромным; и действительно, мы приступаем к определению мощности растущего с огромной скоростью числа 2n где n представляет собой 10 с 46 нулями. Более того, мы можем построить компьютер весом более одного грамма и использовать их дольше чем одну секунду. Но даже люди, привыкшие иметь дело с экспонентальными процессами, могут изумиться следующему аргументу. Предположим, мы используем всю массу нашей планеты Земли, для постройки компьютера и заставим работать в течении всей ее истории. Каким разнообразием будет располагать такая фантастическая машина? Что же заявляет Бриммерман? В году примерно nx10⁷ секунд, возраст земли примерно тысяча миллионов лет. Ее масса около 6х10²⁷ грамм. Тогда такой из всей земли компьютер, за всю историю нашей планеты обработает что-то около 10 ⁹² бит.

Теперь ясно, почему я выбрал разнообразие n=300 для примера о мозге фирмы. За несколько абзацев до этого было показано, что ретикулярное разнообразие, которое может быть генерировано таким умом, при весьма консервативной оценке разнообразия такой фирмы составляет 3х10⁹² бит. А компьютер с массой всей нашей планеты за все время ее существования при идеальном его состоянии и техническом совершенстве может быть использован только для расчета состояний небольшой фирмы.

Состояние фирменной среды, также как и состояние всего человеческого тела, располагает разнообразием значительно большим, чем 300. В живом мозгу, даже по самой ориентировочной оценке разнобразие составит 2^10х6х2^10х7. Если мы хотим действительно разобраться с разнообразием состояний фирмы, то конечно у нас нет никаких оснований полагать, что мозг фирмы нуждается в возможности справляться с меньшим разнообразием, чем это. Ум фирмы, как и ум человека, потенциально может быть в стольких состояниях, чем его проанализировать и исследовать с учетом всех факторов - немыслимо большого числа факторов. Информация об этом должна тогда выдаваться постоянно миллиардами бит и серьезно контролирроваться. Здесь уместно отметить и особо подчеркнуть, что не может и возникать вопроса

О нахождении абсолютного оптимума его поведения - как для человека,так и для фирмы - поскольку нельзя проверить все альтернативы. Из законов природы следует, что это невозможно в принципе.

Но тогда сам анастомотик ретикулум бесполезен. Нужно что-то предпринимать, чтобы держать под контролем всю систему. Должно быть приостановлено растущее разнообразие, его потенциал должен быть сокращен и становиться все меньшим и меньшим, хотя нам неизвестен лучший способ его сокращения. Нет даже разумного пути фиксации и поиска информации в системе такого масштаба, не говоря уже о её обработке на компьютере. Гейнц фон Форестер предложил графическую иллюстрацию проблемы подобного "запоминания". Он подсчитал размер таблицы, которая получится, если перемножить все цифры (всего только) до десяти на все другие цифры (всего только) до десяти. Он предложил также опубликовать результат в справочнике с размером страницы 21 на 28 см на бумаге нормальной толщины. Получается книга толщиной I0¹⁰ сантиметров. И снова математику трудно привыкнуть к такого вида экспоненте. Книжная полка, на которую можно было бы поставить такой справочник, была бы в 100 раз длиннее расстояния от Земли до Солнца. Библиотекарь, который бы бегал вдоль этой полки со скоростью света, утверждает фон Форестер, тратил бы пол дня, чтобы достать нужный том.

Полное управление растущим разнообразием совершенно невозможно для человеческого ума или мозга фирмы. Однако как человек, так и фирма фактически работают. Для этого они уменьшают, они должны уменьшать разнообразие их бесчисленных состояний. Для этого мало веры в компьютер. Вопрос в том, как такие системы спокойно и эффективно справляются с подобной задачей. Ответ таков - путем организации…